2008年1月高等教育自学考试《高等数学(工本)》真题
本试卷总分100分,考试时间150分钟。
一、单项选择题(每小题3分,共15分)
1.设函数f(x,y)=![]() ,则f(
,则f(![]() ,
,![]() )=( )
)=( )
A.
B.
C.
D.
3.设D是由直线x+y+1=0与坐标轴所围成的区域,则二重积分 =( )
=( )
A.0
B.1
C.2
D.4
4.微分方程y'=2y的通解是( )
A.
B.
C.
D.
5.幂级数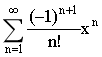 的和函数为( )
的和函数为( )
A.
B.
C.
D.
2.设函数f (x,y) =![]() ,则点(0,0)是f ( x,y )的( )
,则点(0,0)是f ( x,y )的( )
A.间断点
B.连续点
C.极大值点
D.驻点
二、填空题(每小题2分,共10分)
1.设向量α={a,b,b}β={1,-1,1},则α×β=___________.
5.设无穷级数![]() 收敛,则极限
收敛,则极限![]() un=___________.
un=___________.
2.设函数z = sin(x^2+y^2),则![]() =___________.
=___________.
4.微分方程y"=cosx的通解y=___________.
3.二次积分I=![]() 交换积分次序后,I=___________.
交换积分次序后,I=___________.
三、计算题(每小题5分,共60分)
1.设平面![]() 和平面
和平面![]() 求
求![]() 与
与![]() 的夹角.
的夹角.
2.设函数z = xy+![]() ,求全微分dz.
,求全微分dz.
4.求函数f (x,y) =cos ( xy ) +x^2 -y的梯度grad f (1,0).
5.求曲面x^2+2y^2 +z^2=7在点(2,-1,1)处的法线方程.
6.计算二重积分I=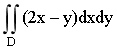 ,其中D是顶点分别为(0,0),(-1,0)(-1,-1)的三角形闭区域.
,其中D是顶点分别为(0,0),(-1,0)(-1,-1)的三角形闭区域.
8.计算对弧长的曲线积分![]() ,其中L是右半圆x2 + y2 = 1(x≥0).
,其中L是右半圆x2 + y2 = 1(x≥0).
10.设函数f (x)满足![]() ,求函数f (x).
,求函数f (x).
11.求无穷级数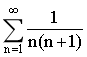 的和.
的和.
12.设函数f(x)=x^2sinx的马克劳林级数为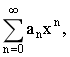 求系数a9.
求系数a9.
3.设方程e^(xy)+ysinx+z^2-2z=1确定函数z=z (x,y),求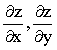 .
.
7.计算三重积分I=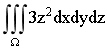 ,其中是旋转抛物面z =x^2+y^2及平面z =1所围成的闭区域.
,其中是旋转抛物面z =x^2+y^2及平面z =1所围成的闭区域.
9.求对坐标的曲线积分![]() 其中L是闭区域D:x^2 +
其中L是闭区域D:x^2 +![]() 的正向边界曲线.
的正向边界曲线.
四、综合题(每小题5分,共15分)
1.欲做容积为4m^3的无盖长方体盒,如何选取长、宽和高,才能使用料最省?
2.求曲面z =2x^2 +y^2和z =6-x^2-2y^2所围立体的体积.
3.设f (x)是以2π为周期的周期函数,它在[-π,π)上的表达式为 f(x)=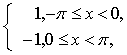 求f (x)的傅里叶级数展开式.
求f (x)的傅里叶级数展开式.
浙江自考网声明:
1、由于各方面情况的调整与变化,本网提供的考试信息仅供参考,考试信息以省考试院及院校官方发布的信息为准。
2、本网信息来源为其他媒体的稿件转载,免费转载出于非商业性学习目的,版权归原作者所有,如有内容与版权问题等请与本站联系。联系邮箱:952056566@qq.com
浙江自考便捷服务
浙江自考网考生群





